Introduction to Control charts.

The control chart is a graph used to study how a process changes over time
Data are plotted in time order
A control chart always has a central line for the average, an upper line for the upper control limit, and a lower line for the lower control limit
Then the graph is divided into zones with each zone at 1 σ , 2 σ , and 3 σ , + or -from the average .

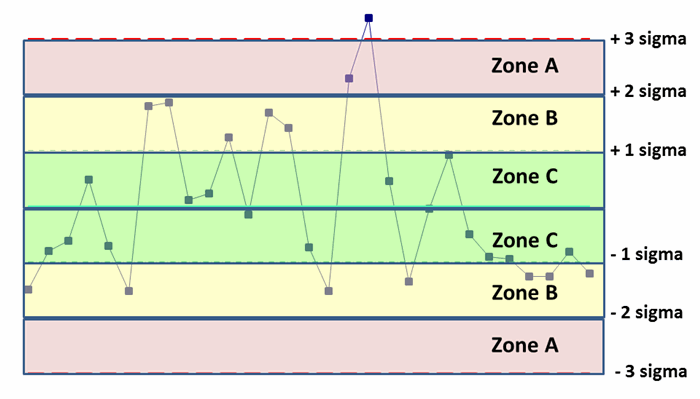
How it works:

Decide a process like to collect 10 samples a day
Find the daily average of the collected samples , example (sum of daily readings)/10
Now follow the below steps to create X and R charts

Lets create a control chart:

X chart:

Application description:

Lets consider data from a temperature sensor ,

The cloumn x1,x2,x3,x4,x5 in below table shows ‘5’ daily readings took from the sensor.

Temperature column shows the daily average of the 5 samples.

so Temperature values are obtained as (x1+x2+x3+x4+x5)/5.

Now follow the below steps:

Note: Here the time column shows sample number ( I should have renamed it in the excel)

Create a normal line chart, with sample number in x axis and temperature in y axis

Now calculate the average (The arithmetic mean) of the average temperature:

Which is : ( sum of all the temperature values) / total entries

(10+20+15+11+12+19+13)/7 , i.e 100/7 = 14.28

Now calculate the deviation of each value from the average/mean.

i.e , 10-14.28, 20 -14.28 etc

Now calculate the square of the difference we got

i.e -4.28^2 , 5.71^ 2 etc

Now calculate the variance

Variance is the mean of ‘square of ‘Difference from mean’‘

i.e (18.36+32.65+0.5+10.7+5.22+22.22+1.65)/7

So the sum of the squares is 13.06122449 and that when divide by 7 we get 1.865889, which is the variance

Now calculate the standard deviation ( sigma σ )

Sigma or standard deviation is just the square root of variance i.e sqrt(1.865889)

Now calculate the UCL and LCL

Now we will calculate the upper and lower control limit which are ( Average + 3 σ ) and (Average – 3 σ ) respectively.

The graph also will be divided into zones ( Average +- σ ) and (Average – 2σ )

Which will be (14.28571429 +/- 1.365976) , (14.28571429 +/- (2 *1.365976) ), (14.28571429 +/- (3* 1.365976) ).

What next:

Now we use this chart to monitor the results

When new results comes in we will see:

whether its inside or outside the limits ,
Is there a pattern in result, for example, all the values are above average ( so we need to re caliber the tool properly)

The chart will be re-calibrated when we have more data and we will recalculate upper and lower limit to make sure that the result are more precise.

R Chart:

R chart considers the range of the sample points

Let us consider similar example above

Here we are taking 5 temperature value samples from the tool daily ( In above case we add this value and divided by 5, to get temperature sample average)

Now calculate ‘Range’ value ‘R’

We get R by subtracting (max-min) from the daily sample set

for example, in first row 33 is the max value and 23 is the min value, so R = 33-23 = 10. Plot it in graph

Now calculate average of R:

Add all the R values, and divide by no of samples : i.e : (10+9+13+….+6)/10 = 100/10=10.

Now calculate the UCL and LCL for R chart:

The equations for finding UCL and LCL for R chart are as below:

UCL = D4 * Rbar
LCL = D3 * Rbar

Were are D4 and D3 are R constants who’s values depends on the number of sample taken daily.

Here values taken per day (n) = 5

and total number of samples (k) = 10 ( we have samples for 10 days)

Now the value of D4 adn D3 depends on ‘n’ and is as below:

reference : https://www.spcforexcel.com/knowledge/variable-control-charts/xbar-r-charts-part-1

Note: no data means ‘0’

So as our ‘n’ value is 5, D3 = 0 and D4 = 2.114, and we have Rbar = 10

Hence,

UCL = 2.114 * 10 = 21.14
LCL = 0*10 = 0

Output:

What next:

Now we use this chart to monitor the results (Range)

When new results comes in we will see:

whether its inside or outside the limits ,
Is there a pattern in result, for example, all the values are above average ( so we need to re caliber the tool properly)

The chart will be re-calibrated when we have more data and we will recalculate upper and lower limit to make sure that the result are more precise.

Note:

You can also calculate UCL and LCL of X chart using Rbar value